Từ thời cổ đại, con người đã luôn bị mê hoặc bởi vẻ đẹp và sự bí ẩn của bầu trời đêm. Những chấm sáng lấp lánh kia đã khơi dậy trong chúng ta niềm khao khát khám phá vũ trụ bao la. Và trong hành trình đầy chông gai đó, Johannes Kepler, nhà thiên văn học người Đức, đã ghi dấu ấn của mình bằng việc khám phá ra ba định luật mang tên ông, đặt nền móng cho thiên văn học hiện đại. Bài viết này sẽ cùng bạn chứng minh định luật keppler 3 và hai định luật còn lại, đồng thời hé lộ những bí mật thú vị về vũ trụ mà chúng ta đang sống.
Định luật 1 Kepler: Quỹ đạo Elip – Vén màn bí ẩn về đường đi của các hành tinh
Trước Kepler, người ta tin rằng các hành tinh di chuyển theo quỹ đạo tròn hoàn hảo quanh Mặt Trời. Tuy nhiên, dựa trên những quan sát tỉ mỉ của Tycho Brahe, Kepler đã phát hiện ra một sự thật khác: các hành tinh chuyển động theo quỹ đạo hình elip, với Mặt Trời nằm ở một trong hai tiêu điểm của elip.
Quỹ đạo elip của hành tinh
Để hiểu rõ hơn về định luật này, chúng ta cần làm quen với một số khái niệm cơ bản:
- Tiêu điểm của elip: Là hai điểm cố định nằm trên trục lớn của elip, có tính chất là tổng khoảng cách từ một điểm bất kỳ trên elip đến hai tiêu điểm luôn bằng một hằng số.
- Trục lớn của elip: Là đoạn thẳng đi qua hai tiêu điểm và cắt elip tại hai điểm, có độ dài lớn nhất trong số tất cả các đoạn thẳng nối hai điểm bất kỳ trên elip.
Sự khác biệt giữa quỹ đạo tròn và quỹ đạo elip chính là độ lệch tâm (e). Độ lệch tâm là tỉ số giữa khoảng cách từ tâm elip đến một tiêu điểm với độ dài bán trục lớn. Đối với đường tròn, độ lệch tâm bằng 0, trong khi đối với elip, độ lệch tâm nằm trong khoảng từ 0 đến 1.
Vậy tại sao các hành tinh lại chuyển động theo quỹ đạo elip?
Câu trả lời nằm ở lực hấp dẫn giữa Mặt Trời và các hành tinh. Lực này tỉ lệ nghịch với bình phương khoảng cách giữa chúng, có nghĩa là khi hành tinh ở gần Mặt Trời, lực hấp dẫn mạnh hơn và ngược lại. Chính sự thay đổi về lực hấp dẫn này đã tạo nên quỹ đạo elip.
Định luật 2 Kepler: Bảo toàn Mômen Động lượng – Bí mật về tốc độ của các hành tinh
Định luật 2 Kepler phát biểu rằng: Đường thẳng nối Mặt Trời với một hành tinh quét những diện tích bằng nhau trong những khoảng thời gian bằng nhau.
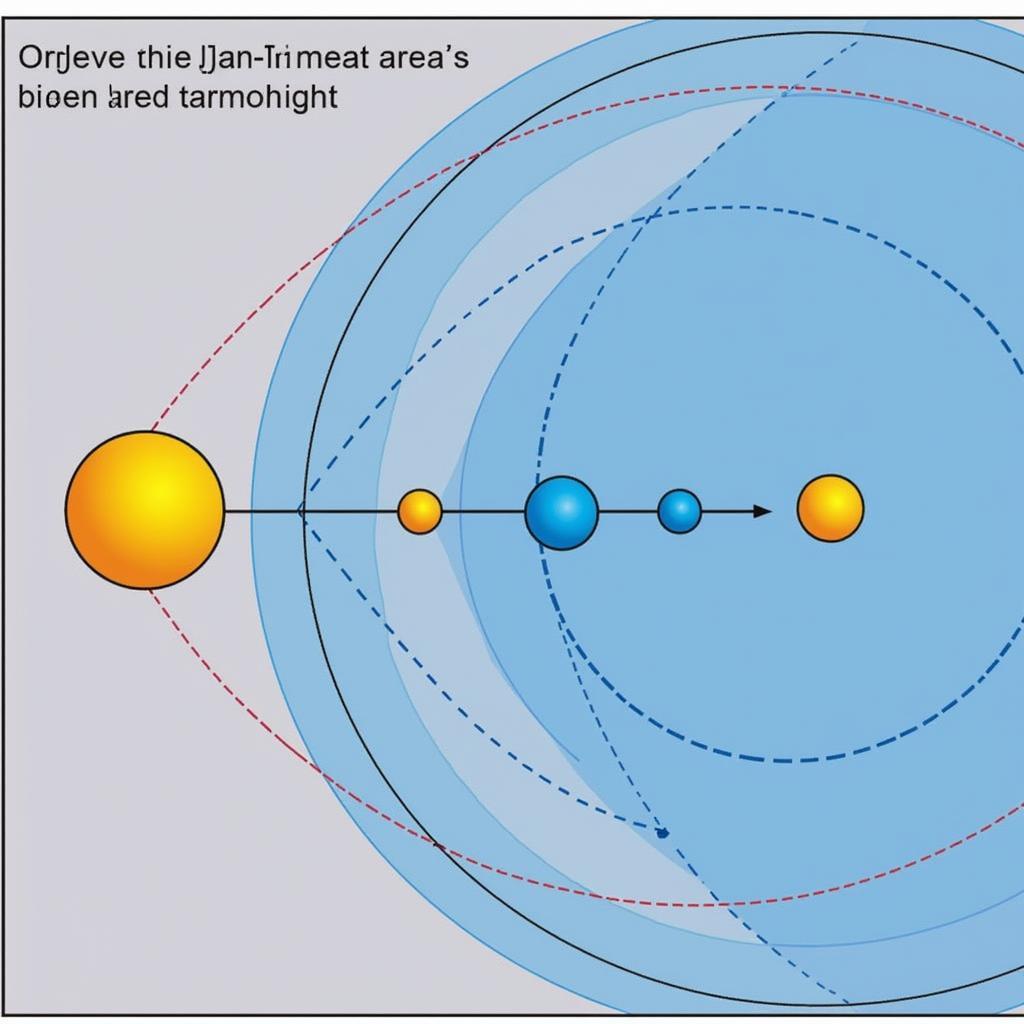Minh họa Định luật 2 Kepler
Điều này có nghĩa là khi hành tinh ở gần Mặt Trời hơn, nó sẽ di chuyển nhanh hơn và khi ở xa Mặt Trời hơn, nó sẽ di chuyển chậm hơn.
Hãy hình dung một hành tinh đang di chuyển trên quỹ đạo elip quanh Mặt Trời. Khi hành tinh ở gần Mặt Trời, lực hấp dẫn mạnh hơn, kéo hành tinh về phía nó với tốc độ nhanh hơn. Ngược lại, khi hành tinh ở xa Mặt Trời, lực hấp dẫn yếu hơn, khiến hành tinh di chuyển chậm hơn.
Định luật 2 Kepler cho thấy mômen động lượng của một hành tinh quanh Mặt Trời là một đại lượng bảo toàn. Mômen động lượng là đại lượng vật lý đặc trưng cho khả năng tiếp tục quay của vật, phụ thuộc vào khối lượng, vận tốc và khoảng cách so với trục quay.
Định luật 3 Kepler: Hòa âm của Vũ trụ – Mối liên hệ giữa Chu kỳ Quỹ đạo và Khoảng cách
Định luật 3 Kepler là đỉnh cao trong công trình nghiên cứu của ông, thiết lập mối quan hệ toán học giữa chu kỳ quỹ đạo của một hành tinh và khoảng cách trung bình của nó đến Mặt Trời. Cụ thể, định luật này phát biểu: Bình phương chu kỳ quỹ đạo của một hành tinh tỷ lệ với lập phương bán trục lớn của quỹ đạo elip.
Công thức toán học của định luật 3 Kepler:
T^2 = (4π^2/GM) a^3Trong đó:
- T là chu kỳ quỹ đạo của hành tinh (đơn vị: năm)
- a là bán trục lớn của quỹ đạo elip (đơn vị: đơn vị thiên văn – AU, với 1 AU là khoảng cách trung bình giữa Trái Đất và Mặt Trời)
- G là hằng số hấp dẫn
- M là khối lượng của Mặt Trời
Định luật 3 Kepler cho phép các nhà thiên văn học tính toán được khoảng cách giữa các hành tinh với Mặt Trời một cách chính xác, từ đó vén màn bí mật về kích thước của hệ Mặt Trời và khoảng cách giữa các thiên thể.
Kết luận
Ba định luật Kepler đã tạo nên một cuộc cách mạng trong thiên văn học, thay đổi hoàn toàn cách chúng ta nhìn nhận về vũ trụ. Không chỉ đơn thuần là những công thức toán học, chúng còn là minh chứng cho sự hòa âm và trật tự của vũ trụ, khơi dậy trong con người niềm đam mê khám phá những bí ẩn của không gian bao la.
Bạn có muốn tìm hiểu thêm về các định luật kepler? Hãy cùng chúng tôi tiếp tục hành trình khám phá những điều kỳ diệu của vũ trụ nhé!