Định luật Kepler 2, còn được gọi là định luật về diện tích, là một trong ba định luật Kepler mô tả chuyển động của các hành tinh quanh Mặt Trời. Định luật này khẳng định rằng đường nối giữa một hành tinh và Mặt Trời quét những diện tích bằng nhau trong những khoảng thời gian bằng nhau. Việc Chứng Minh định Luật Kepler 2 không chỉ giúp chúng ta hiểu rõ hơn về vũ trụ mà còn là một ví dụ tuyệt vời về ứng dụng của các nguyên lý vật lý cơ bản.
Cùng tìm hiểu sâu hơn về cách chứng minh định luật Kepler 2 và những ý nghĩa quan trọng của nó trong việc nghiên cứu thiên văn học. Xem thêm về biểu thức định luật kepler.
Định Luật Kepler 2 Là Gì?
Định luật Kepler 2 phát biểu rằng: Một đoạn thẳng nối một hành tinh và Mặt Trời quét những diện tích bằng nhau trong những khoảng thời gian bằng nhau. Điều này có nghĩa là khi hành tinh ở gần Mặt Trời, nó di chuyển nhanh hơn so với khi nó ở xa Mặt Trời.
Chứng Minh Định Luật Kepler 2 Bằng Toán Học
Chứng minh định luật Kepler 2 dựa trên nguyên lý bảo toàn mô men động lượng. Mô men động lượng của một hành tinh quanh Mặt Trời là không đổi vì lực hấp dẫn giữa chúng là lực hướng tâm.
Ta có thể biểu diễn mô men động lượng (L) của hành tinh như sau: L = mvr, trong đó m là khối lượng của hành tinh, v là vận tốc của hành tinh, và r là khoảng cách từ hành tinh đến Mặt Trời.
Diện tích (dA) quét bởi vectơ bán kính trong một khoảng thời gian nhỏ (dt) được tính bằng: dA = (1/2)r²dθ, với dθ là góc quét bởi vectơ bán kính trong thời gian dt.
Tốc độ diện tích (dA/dt) được tính bằng: dA/dt = (1/2)r²(dθ/dt) = (1/2)rv, với v = rdθ/dt là vận tốc tiếp tuyến của hành tinh.
Vì mô men động lượng được bảo toàn (L = hằng số), ta có L = mrv = hằng số. Do đó, dA/dt = L/(2m) = hằng số. Điều này chứng minh rằng tốc độ diện tích là hằng số, nghĩa là diện tích quét bởi vectơ bán kính trong những khoảng thời gian bằng nhau là bằng nhau.
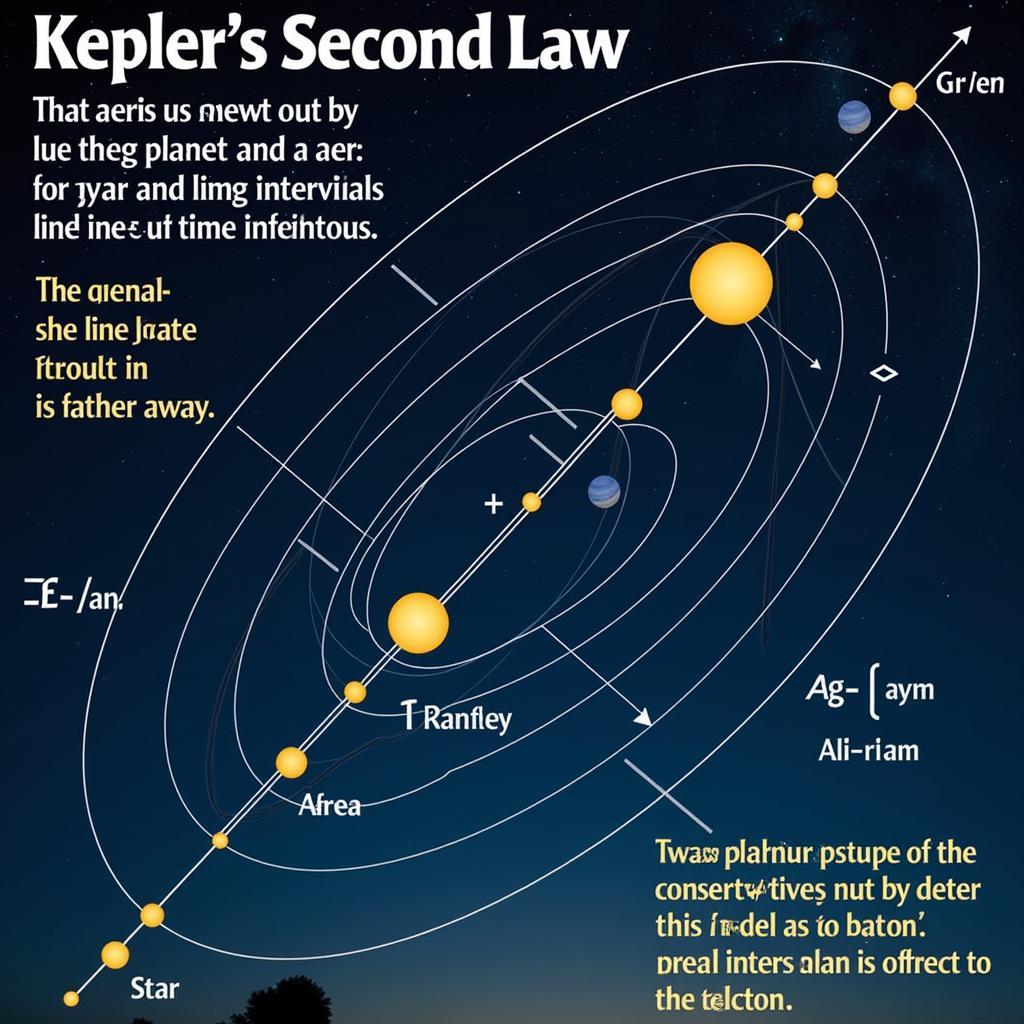Minh họa định luật Kepler 2
Ý Nghĩa Của Định Luật Kepler 2
Định luật Kepler 2 có ý nghĩa quan trọng trong việc hiểu chuyển động của các hành tinh và các vật thể khác trong hệ Mặt Trời. Nó giúp chúng ta dự đoán vị trí của các hành tinh và thiết kế các sứ mệnh không gian.
Tìm hiểu thêm về bài tập ba định luật kepler.
Tại Sao Hành Tinh Chuyển Động Nhanh Hơn Khi Gần Mặt Trời?
Khi hành tinh ở gần Mặt Trời, lực hấp dẫn mạnh hơn, làm tăng tốc độ của nó. Ngược lại, khi hành tinh ở xa Mặt Trời, lực hấp dẫn yếu hơn, làm giảm tốc độ của nó. Đây là lý do tại sao hành tinh chuyển động nhanh hơn khi gần Mặt Trời và chậm hơn khi xa Mặt Trời.
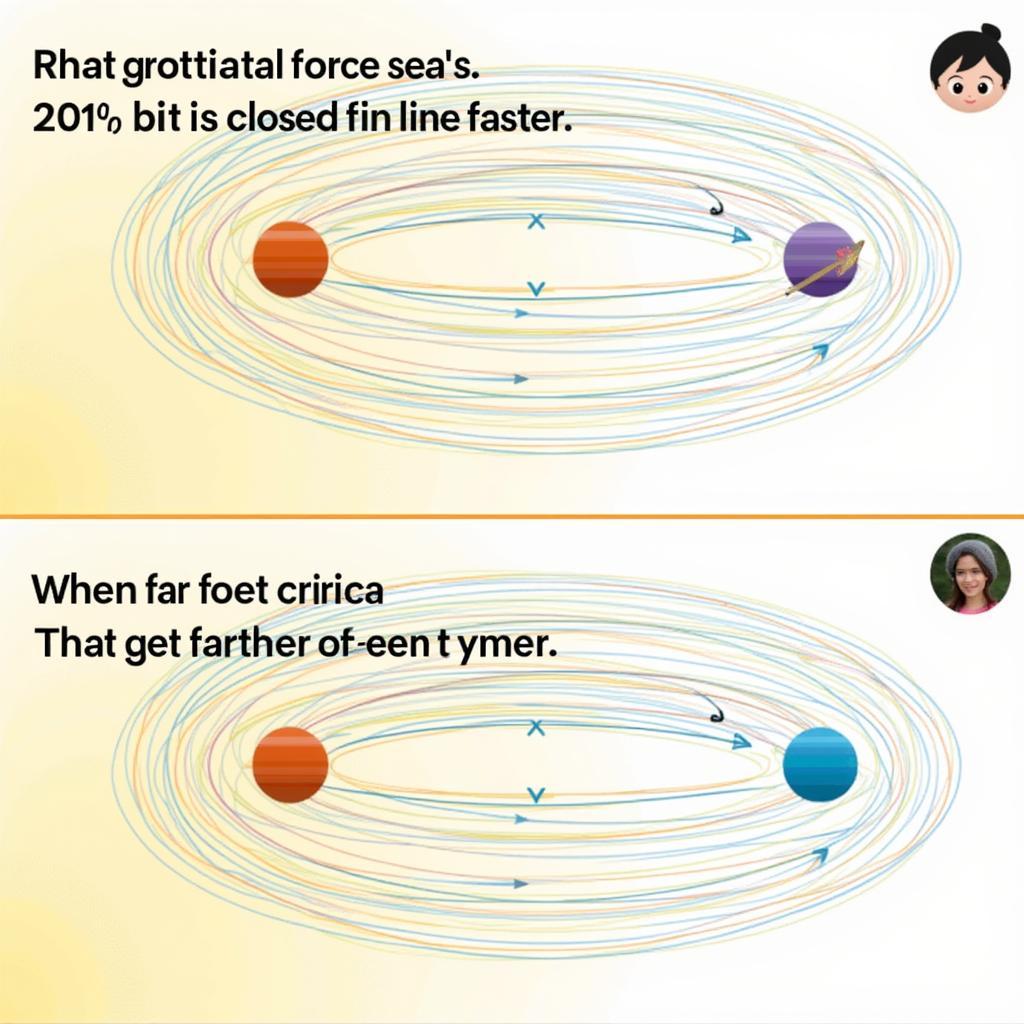So sánh tốc độ hành tinh ở các vị trí khác nhau trên quỹ đạo
Giáo sư Nguyễn Văn A, chuyên gia vật lý thiên văn tại Đại học Quốc gia Hà Nội, chia sẻ: “Định luật Kepler 2 là một trong những khám phá quan trọng nhất trong lịch sử thiên văn học. Nó giúp chúng ta hiểu rõ hơn về sự vận hành của vũ trụ.”
Kết Luận
Chứng minh định luật Kepler 2 không chỉ là một bài toán vật lý thú vị mà còn là chìa khóa để hiểu sâu hơn về chuyển động của các hành tinh trong hệ Mặt Trời. Nó cho thấy sự kết hợp hài hòa giữa toán học và quan sát thực nghiệm, mở ra những cánh cửa mới cho việc khám phá vũ trụ. Bạn muốn tìm hiểu thêm về người đã ai phát minh ra định luật vạn vật hấp dẫn? Hãy xem bài viết liên quan trên trang web của chúng tôi.
Ứng dụng định luật Kepler 2 trong tính toán quỹ đạo vệ tinh
Xem thêm chứng minh 3 định luật kepler.
FAQ
- Định luật Kepler 2 áp dụng cho vật thể nào? Định luật Kepler 2 áp dụng cho tất cả các vật thể quay quanh một tâm lực hấp dẫn.
- Định luật Kepler 2 có liên quan gì đến định luật 1 và 3? Cả ba định luật Kepler đều mô tả chuyển động của các hành tinh quanh Mặt Trời.
- Ai là người phát hiện ra định luật Kepler 2? Johannes Kepler là người phát hiện ra định luật Kepler 2.
- Định luật Kepler 2 có ý nghĩa gì trong thực tế? Định luật Kepler 2 được sử dụng để tính toán quỹ đạo của vệ tinh và tàu vũ trụ.
- Làm thế nào để chứng minh định luật Kepler 2 một cách đơn giản? Có thể chứng minh định luật Kepler 2 bằng cách sử dụng nguyên lý bảo toàn mô men động lượng.
- Định luật Kepler 2 có đúng với tất cả các hệ hành tinh? Đúng, định luật Kepler 2 áp dụng cho tất cả các hệ hành tinh.
- Có những ngoại lệ nào cho định luật Kepler 2? Không có ngoại lệ nào cho định luật Kepler 2 trong phạm vi của cơ học cổ điển.
Bạn có câu hỏi nào khác không? Hãy xem các bài viết khác trên web của chúng tôi.
Khi cần hỗ trợ hãy liên hệ Số Điện Thoại: 0936238633, Email: [email protected] Hoặc đến địa chỉ: 408 An Tiêm, Hà Khẩu, Hạ Long, Quảng Ninh, Việt Nam. Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.
