Luật phân phối chuẩn, hay còn gọi là phân phối Gauss, là một khái niệm quan trọng trong thống kê. Việc bấm máy luật phân phối chuẩn giúp chúng ta tính toán xác suất của các biến ngẫu nhiên liên tục. Bài viết này sẽ hướng dẫn bạn cách bấm máy tính luật phân phối chuẩn một cách chi tiết và hiệu quả.
Hiểu Về Luật Phân Phối Chuẩn
Luật phân phối chuẩn được mô tả bằng một đường cong hình chuông đối xứng, với giá trị trung bình nằm ở đỉnh. Độ rộng của đường cong được xác định bởi độ lệch chuẩn. Phân phối chuẩn có ứng dụng rộng rãi trong nhiều lĩnh vực, từ khoa học tự nhiên đến kinh tế xã hội. Việc nắm vững cách bấm máy luật phân phối chuẩn là rất cần thiết để phân tích dữ liệu và đưa ra quyết định dựa trên bằng chứng.
Hướng Dẫn Bấm Máy Luật Phân Phối Chuẩn
Tùy thuộc vào loại máy tính bạn sử dụng (Casio, Vinacal, Texas Instruments, v.v.), các bước bấm máy có thể hơi khác nhau. Tuy nhiên, nguyên tắc chung là sử dụng các hàm tích hợp sẵn để tính toán xác suất. Dưới đây là hướng dẫn chung cho một số loại máy tính phổ biến:
Bấm Máy Casio
- Nhấn Mode, chọn STAT.
- Chọn DIST (Distribution).
- Chọn Ncd (Normal Cumulative Distribution).
- Nhập các giá trị: Lower (giá trị dưới), Upper (giá trị trên), σ (độ lệch chuẩn), μ (giá trị trung bình).
- Nhấn “=” để tính toán xác suất.
Bấm Máy Vinacal
- Nhấn Mode, chọn STAT.
- Chọn DIST.
- Chọn NORM.
- Nhập các giá trị tương tự như Casio.
Bấm Máy Texas Instruments
Các dòng máy tính Texas Instruments thường có chức năng normalcdf trong menu phân phối thống kê. Bạn cần nhập các giá trị lower, upper, mean (giá trị trung bình), và standard deviation (độ lệch chuẩn) để tính toán.
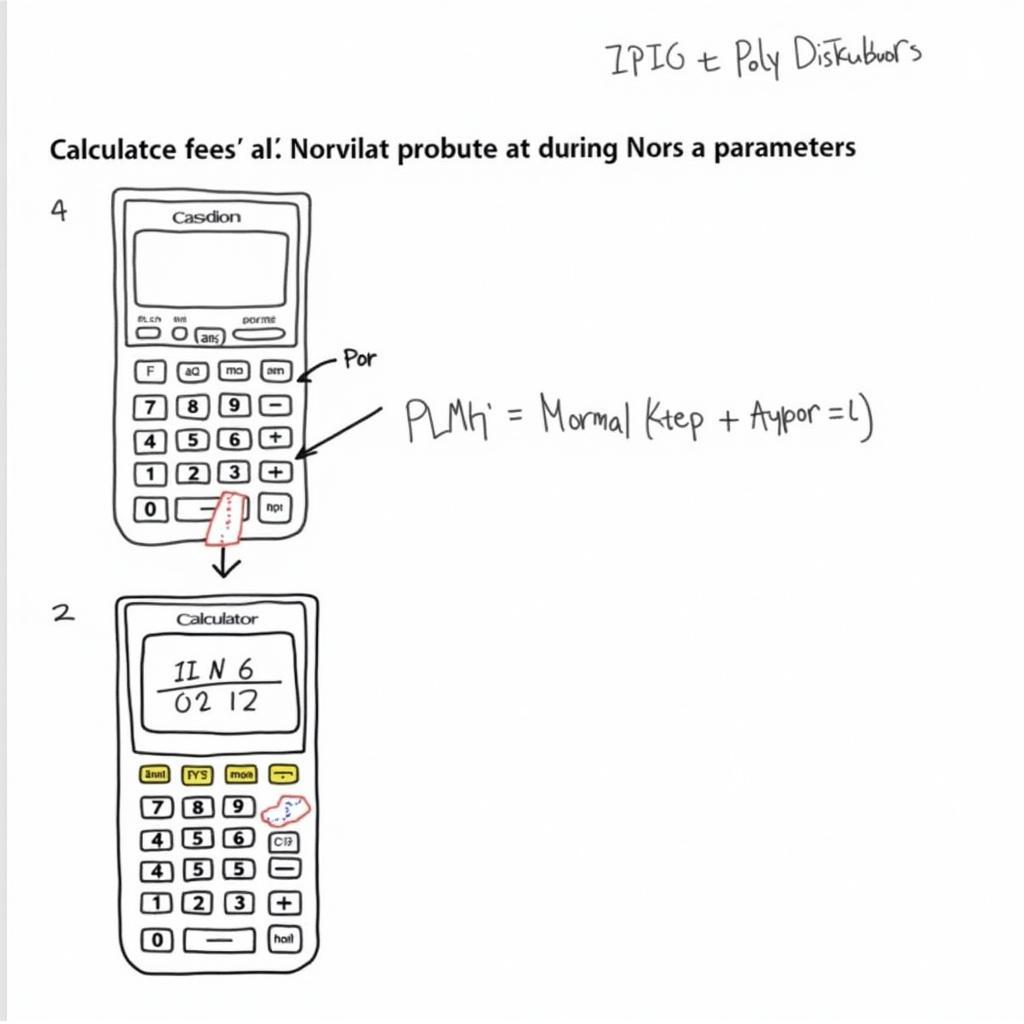Cách bấm máy tính Casio phân phối chuẩn
Các Ví Dụ Về Bấm Máy Luật Phân Phối Chuẩn
Để hiểu rõ hơn về cách áp dụng, hãy xem xét một vài ví dụ cụ thể:
-
Ví dụ 1: Một biến ngẫu nhiên X tuân theo luật phân phối chuẩn với giá trị trung bình μ = 10 và độ lệch chuẩn σ = 2. Tính xác suất P(8 < X < 12).
-
Ví dụ 2: Điểm thi của một kỳ thi tuân theo phân phối chuẩn với μ = 70 và σ = 10. Tính xác suất để một học sinh đạt điểm trên 80.
Tính xác suất phân phối chuẩn với ví dụ cụ thể
Một Số Lưu Ý Khi Bấm Máy
- Đảm bảo bạn đã nhập đúng các giá trị cho μ và σ.
- Chú ý đến đơn vị đo của các biến.
- Kiểm tra lại kết quả bằng cách sử dụng bảng phân phối chuẩn hoặc phần mềm thống kê.
“Việc thành thạo bấm máy luật phân phối chuẩn là một kỹ năng quan trọng cho bất kỳ ai làm việc với dữ liệu thống kê,” – Nguyễn Văn A, Giảng viên Thống kê, Đại học X.
Ứng Dụng Của Luật Phân Phối Chuẩn
Luật phân phối chuẩn có rất nhiều ứng dụng trong thực tế, bao gồm:
- Kiểm định giả thuyết: Đánh giá tính đúng đắn của một giả thuyết dựa trên dữ liệu mẫu.
- Ước lượng khoảng tin cậy: Xác định khoảng giá trị mà tham số tổng thể có thể nằm trong đó.
- Phân tích hồi quy: Mô hình hóa mối quan hệ giữa các biến.
Ứng dụng phân phối chuẩn trong thực tế
Kết Luận
Bấm máy luật phân phối chuẩn là một kỹ năng cần thiết trong thống kê. Hy vọng bài viết này đã cung cấp cho bạn những hướng dẫn chi tiết và hữu ích. Nắm vững kỹ năng này sẽ giúp bạn phân tích dữ liệu một cách hiệu quả và đưa ra quyết định chính xác hơn.
FAQ
- Luật phân phối chuẩn là gì?
- Tại sao cần phải bấm máy luật phân phối chuẩn?
- Làm thế nào để nhập dữ liệu vào máy tính?
- Các loại máy tính nào có thể bấm máy luật phân phối chuẩn?
- Tôi có thể tìm thấy bảng phân phối chuẩn ở đâu?
- Có phần mềm nào hỗ trợ tính toán phân phối chuẩn không?
- Làm thế nào để kiểm tra kết quả tính toán?
Mô tả các tình huống thường gặp câu hỏi.
Người dùng thường gặp khó khăn trong việc xác định đúng hàm cần sử dụng trên máy tính và nhập chính xác các tham số. Việc hiểu rõ khái niệm về giá trị dưới, giá trị trên, độ lệch chuẩn và giá trị trung bình là rất quan trọng.
Gợi ý các câu hỏi khác, bài viết khác có trong web.
Bạn có thể tìm hiểu thêm về các chủ đề liên quan như kiểm định giả thuyết, ước lượng khoảng tin cậy, và phân tích hồi quy trên website của chúng tôi.
