Bài Tập Chuyên Đề Định Luật Bảo Toàn Cơ Năng

Định luật bảo toàn cơ năng là một nguyên lý quan trọng trong vật lý, đặc biệt là trong lĩnh vực cơ học. Bài viết này sẽ đi sâu vào phân tích định luật bảo toàn cơ năng, đồng thời cung cấp các bài tập chuyên đề giúp bạn nắm vững kiến thức này.

Hiểu Rõ Định Luật Bảo Toàn Cơ Năng

Định luật bảo toàn cơ năng phát biểu rằng trong một hệ kín, không có ma sát và các lực không thế khác, tổng cơ năng của hệ luôn được bảo toàn. Cơ năng là tổng của động năng và thế năng. Động năng liên quan đến chuyển động của vật, trong khi thế năng liên quan đến vị trí của vật trong trường lực.

Phân Loại Bài Tập Chuyên Đề Định Luật Bảo Toàn Cơ Năng

Bài tập về định luật bảo toàn cơ năng thường được chia thành các dạng sau:

• Vật rơi tự do: Đây là dạng bài tập cơ bản nhất, xét chuyển động của vật dưới tác dụng của trọng lực.
• Vật trượt trên mặt phẳng nghiêng: Dạng bài tập này phức tạp hơn, xét đến góc nghiêng và lực ma sát (nếu có).
• Con lắc đơn: Bài tập con lắc đơn thường liên quan đến chuyển động dao động và sự chuyển hóa giữa động năng và thế năng.
• Con lắc lò xo: Tương tự con lắc đơn, bài tập con lắc lò xo cũng liên quan đến dao động và sự chuyển hóa năng lượng.

Phương Pháp Giải Bài Tập Định Luật Bảo Toàn Cơ Năng

Để giải bài tập về định luật bảo toàn cơ năng, ta thường áp dụng các bước sau:

1. Xác định hệ kín: Đảm bảo hệ không chịu tác dụng của ngoại lực không thế (như lực ma sát).
2. Xác định trạng thái ban đầu và trạng thái cuối: Ghi nhận các thông tin về vận tốc, vị trí, độ cao của vật ở hai thời điểm này.
3. Áp dụng định luật bảo toàn cơ năng: Viết phương trình thể hiện tổng cơ năng ở trạng thái ban đầu bằng tổng cơ năng ở trạng thái cuối: W_đầu + W_{t đầu} = W_{đ cuối} + W_{t cuối}.
4. Giải phương trình: Tìm các đại lượng chưa biết.

Ví dụ Bài Tập Định Luật Bảo Toàn Cơ Năng

Một vật có khối lượng m = 1kg được thả rơi tự do từ độ cao h = 10m. Tính vận tốc của vật khi chạm đất. Bỏ qua sức cản của không khí.

• Trạng thái ban đầu: v_đầu = 0 (vật bắt đầu rơi), h_đầu = 10m
• Trạng thái cuối: v_cuối = ?, h_cuối = 0 (vật chạm đất)

Áp dụng định luật bảo toàn cơ năng: mgh_đầu = 1/2mv_cuối²

Từ đó, ta tính được v_cuối = √(2gh) = √(29.810) ≈ 14 m/s.

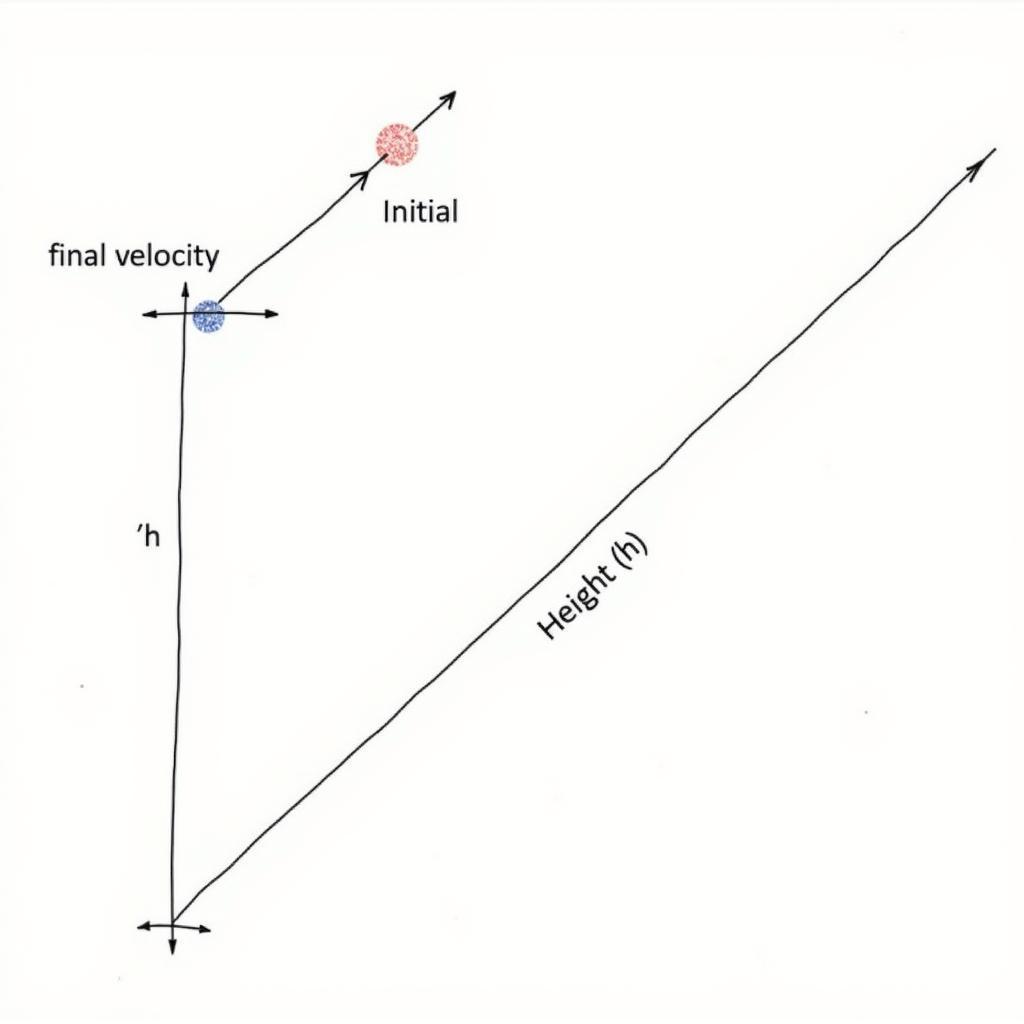Ví Dụ Bài Tập Định Luật Bảo Toàn Cơ Năng

Bài Tập Chuyên Đề Định Luật Bảo Toàn Cơ Năng Nâng Cao

Các bài tập nâng cao thường kết hợp định luật bảo toàn cơ năng với các kiến thức khác như định luật II Newton, chuyển động ném xiên, hoặc xét đến lực ma sát.

Ví dụ: Một vật trượt không vận tốc đầu từ đỉnh một mặt phẳng nghiêng có góc nghiêng α. Hệ số ma sát giữa vật và mặt phẳng nghiêng là μ. Tính vận tốc của vật khi đến chân mặt phẳng nghiêng.

Giải quyết bài toán này đòi hỏi phải xét đến công của lực ma sát, làm giảm cơ năng của hệ.

Kết luận

Bài Tập Chuyên đề định Luật Bảo Toàn Cơ Năng giúp người học hiểu sâu và vận dụng linh hoạt định luật này trong các tình huống thực tế. Bằng cách luyện tập thường xuyên, bạn sẽ nắm vững kiến thức và nâng cao khả năng giải quyết vấn đề.

FAQ

1. Định luật bảo toàn cơ năng áp dụng trong trường hợp nào?
2. Thế nào là hệ kín?
3. Động năng và thế năng là gì?
4. Làm sao để tính động năng và thế năng?
5. Tại sao cơ năng không được bảo toàn khi có ma sát?
6. Có những dạng bài tập nào về định luật bảo toàn cơ năng?
7. Làm thế nào để giải bài tập về con lắc đơn và con lắc lò xo?

Gợi ý các câu hỏi khác, bài viết khác có trong web.

• Định luật bảo toàn động lượng là gì?
• Sự khác nhau giữa định luật bảo toàn cơ năng và định luật bảo toàn động lượng?
• Các bài tập vận dụng định luật bảo toàn động lượng.