Chứng Minh Định Luật Menclaus: Từ Lý Thuyết Đến Ứng Dụng Thực Tế

Định luật Menclaus, một định lý kinh điển trong hình học phẳng, đã và đang thu hút sự quan tâm của rất nhiều người yêu toán học. Bài viết này sẽ đi sâu vào tìm hiểu về định luật Menclaus, từ cách chứng minh cho đến những ứng dụng thực tế của nó trong đời sống.

Định Luật Menclaus Là Gì?

Định luật Menclaus được phát biểu như sau: Cho tam giác ABC và ba điểm D, E, F lần lượt nằm trên các đường thẳng chứa ba cạnh BC, CA, AB. Ba điểm D, E, F thẳng hàng khi và chỉ khi:

(BD/DC) * (CE/EA) * (AF/FB) = -1

Trong đó, tỉ số giữa hai đoạn thẳng được tính theo hướng (ví dụ BD/DC là tỉ số giữa độ dài đoạn thẳng có hướng BD và độ dài đoạn thẳng có hướng DC).

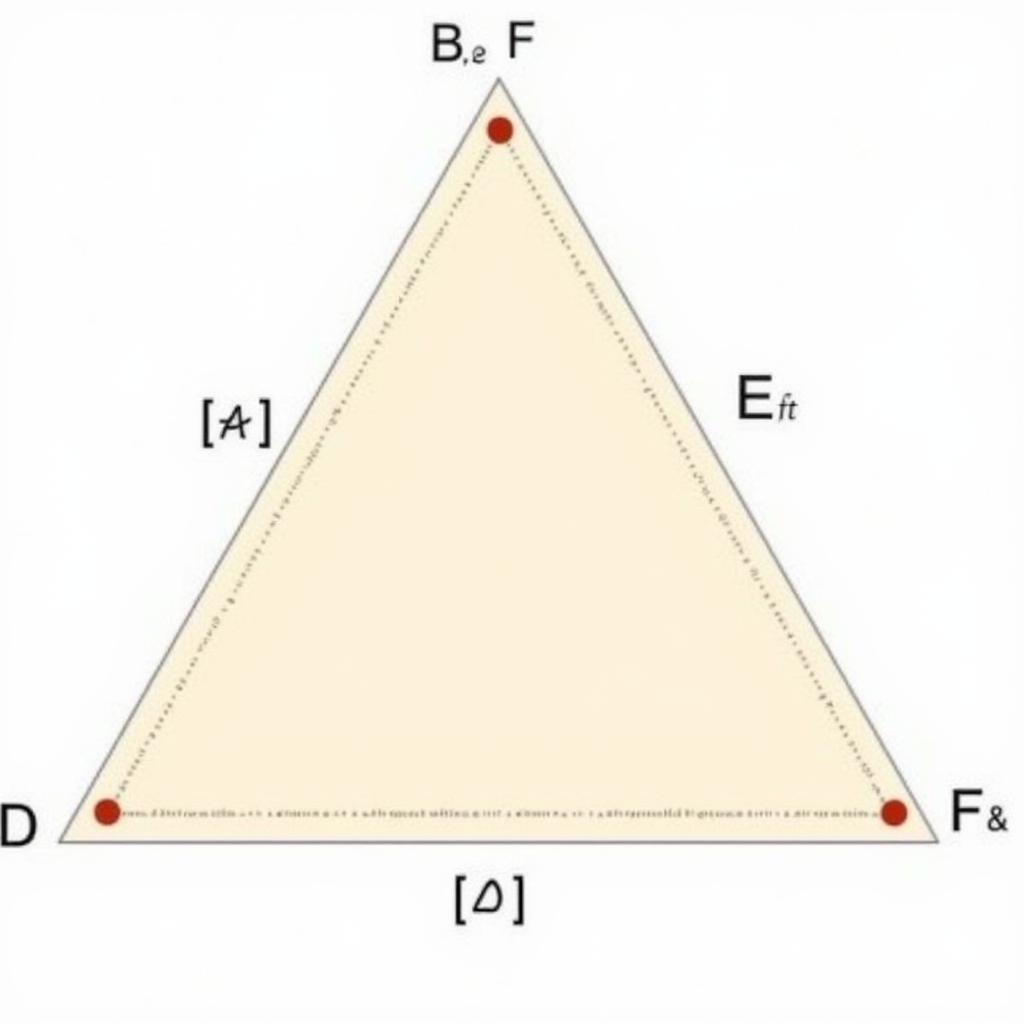Minh họa Định luật Menclaus

Chứng Minh Định Luật Menclaus

Có nhiều cách để Chứng Minh định Luật Menclaus, một trong những cách chứng minh đơn giản nhất là sử dụng diện tích của tam giác:

1. Xét trường hợp ba điểm D, E, F thẳng hàng: Gọi O là giao điểm của AD và BE. Ta có:

   • S(BOD)/S(COD) = BD/DC (chung chiều cao từ O)
   • S(COE)/S(AOE) = CE/EA (chung chiều cao từ O)
   • S(AOF)/S(BOF) = AF/FB (chung chiều cao từ O)

   Nhân ba vế của ba đẳng thức trên, ta được:

   (BD/DC) * (CE/EA) * (AF/FB) = (S(BOD)/S(COD)) * (S(COE)/S(AOE)) * (S(AOF)/S(BOF))
                            = (S(BOD) * S(COE) * S(AOF)) / (S(COD) * S(AOE) * S(BOF))
                            = 1

   Do D, E, F thẳng hàng nên O nằm trên đường thẳng DF, do đó tỉ số diện tích cuối cùng bằng -1. Vậy ta có:

   (BD/DC) * (CE/EA) * (AF/FB) = -1

2. Xét trường hợp (BD/DC) (CE/EA) (AF/FB) = -1: Giả sử AD cắt BE tại O. Qua C vẽ đường thẳng song song với DF, cắt AB tại F’. Ta cần chứng minh F trùng với F’.

   • Áp dụng định lý Thales, ta có: BD/DC = BF’/F’A.
   • Từ giả thiết (BD/DC) (CE/EA) (AF/FB) = -1, ta suy ra (BF’/F’A) (CE/EA) (AF/FB) = -1.
   • Do đó (CE/EA) (AF/FB) = -F’A/BF’, hay (CE/EA) = (-F’A/BF’) (FB/AF) = F’C/F’B.

   Theo định lý Menelaus (đã chứng minh ở trường hợp 1), ba điểm D, E, F’ thẳng hàng. Do đó, F’ trùng với F. Vậy ta có điều phải chứng minh.

Ứng Dụng Của Định Luật Menclaus

Ứng dụng của định luật Menclaus

Định luật Menclaus là một công cụ hữu ích trong việc giải quyết các bài toán hình học phẳng, đặc biệt là các bài toán liên quan đến sự thẳng hàng của ba điểm. Ngoài ra, định luật này còn được ứng dụng trong một số lĩnh vực khác như:

• Vật lý: Định luật Menclaus được sử dụng trong các bài toán về cơ học, quang học, và điện từ học.
• Khoa học máy tính: Định luật Menclaus được ứng dụng trong lĩnh vực đồ họa máy tính và xử lý ảnh.
• Kiến trúc và xây dựng: Định luật Menclaus được sử dụng trong việc thiết kế và xây dựng các công trình kiến trúc.

Kết Luận

Định luật Menclaus là một định lý quan trọng trong hình học phẳng, nó cung cấp một công cụ mạnh mẽ để giải quyết các bài toán liên quan đến sự thẳng hàng của ba điểm. Với những ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau, định luật Menclaus đã và đang khẳng định được vai trò quan trọng của mình trong toán học và đời sống.

Câu hỏi thường gặp

1. Định luật Menclaus có áp dụng cho tam giác vuông không?

   Có, định luật Menclaus áp dụng cho mọi loại tam giác, bao gồm cả tam giác vuông.

2. Định luật Menclaus có liên quan gì đến định lý Ceva không?

   Định luật Menclaus và định lý Ceva đều là những định lý quan trọng trong hình học phẳng. Định lý Ceva phát biểu về điều kiện cần và đủ để ba đường thẳng đồng quy, trong khi định luật Menclaus phát biểu về điều kiện cần và đủ để ba điểm thẳng hàng.

Bạn cần hỗ trợ thêm?

Hãy liên hệ với chúng tôi!

• Số Điện Thoại: 0936238633
• Email: [email protected]
• Địa chỉ: 408 An Tiêm, Hà Khẩu, Hạ Long, Quảng Ninh, Việt Nam.

Chúng tôi có đội ngũ chăm sóc khách hàng 24/7.